Inversive plane

An inversive plane is a class of incidence structure in mathematics.

It may be axiomatised by taking two classes, "points" and "circles" (or "blocks") with the properties

• any three points lie on exactly one circle;
• if P and Q are points and c a circle with P on c and Q not, then there is exactly one circle e containing P and Q and intersecting c only in P;
• there are four points not all on the same circle.

The finite inversive planes are precisely the 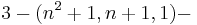designs. Such a design is always a Steiner system.

Ovoids

When one takes as points the points of an ovoid in PG(3,q), with q a prime power, and as blocks the planes that are not tangent to the ovoid, one finds a 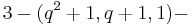design.

Inversive planes that arise in this way are said to be egglike. Dembowksi proved that when n is even, every inversive plane is egglike (and thus n is a power of 2). It is not known to be true when n is odd.

Derived designs and extensions

Inversive planes are precisely the extensions of the 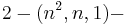designs or hence the affine planes.

References

• E.F. Assmus Jr and J.D. Key, Designs and their codes, Cambridge University Press, ISBN 0-521-45839-0. p. 309-312.
• P. Dembowski, Finite geometries, Springer Verlag, 1968, repr.1996, ISBN 3540617868.
• D.R. Hughes and F.C. Piper, Design theory, Cambridge University Press, ISBN 0-521-35872-8. p. 133-136.